《Weakly supervised discriminative feature learning with state information for...

Re-ID CVPR

字数统计: 1.4k阅读时长: 5 min

 2020/07/04 

Introduction

由于人工标注的代价十分高昂，对于可判别性视觉特征的无监督学习是一个非常具有吸引力的课题。不同状态（例如相机视角、人物姿势等）下同一个体的不同图像可能会有一定的差异，这样的差异为无监督学习带来了不小的挑战。
本篇论文提出了简单的伪标注模型，并提出一种使用状态信息作为弱监督条件的决策边界修正方法和特征漂移正则化方法。

Weakly supervised Discriminative Learning with State Information

Basic Model

定义 $\mathcal{U}=\{u_i\}_{i=1}^N$ 代表输入的未标注数据集， $u_i$ 代表一张未标注的图像， $s_i\in \{1,\cdots,J\}$ 代表图像的状态信息，例如光照。改论文希望能够学习到一个深度神经网络 $f$ 将输入图像编码到一个深度特征空间，定义特征编码为 $x$ ，即 $x=f(u;\theta)$ ，其中 $\theta$ 代表网络的参数。
进一步的，对于每一个特征空间下的编码 $x$ ，可以假定其属于一个代理类之中，这个分类任务可以由一个代理分类器 $\mu$ 完成。此时，这一判别学习任务可以被视作代理分类器的分类任务。
$\mathop{\min}_{\theta,\{\mu_k\}}L_{surr}=-\sum_{x}\log\frac{\exp(x^\top \mu_{\hat{y}})}{\sum_{k=1}{K}\exp(x^\top \mu_k)}$
上式中 $\hat{y}$ 代表 $x$ 所属的代理类，可以通过下式获得
$\hat{y}=\mathop{\arg\mathop{\max}_{k}}\exp(x^\top \mu_{k})$
然而这样的代理类划分并不总是正确的，部分图像质量较差，存在失真，可能使该图像错误地跨越决策边界，被划分到其他类别，出现局部的错误；更普遍的，一些环境因素，例如低光照，可能使图像的可判别性更差，使得一批相同状态的图像同时朝同样的方向发生偏移。
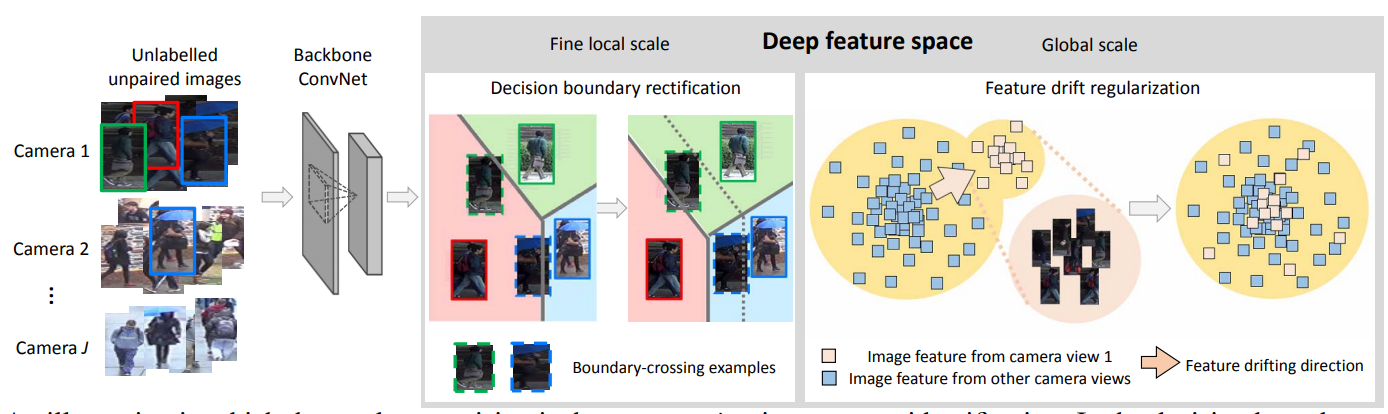
针对上述问题，论文设计了以下两种策略来解决这两个问题：
1. 弱监督条件下的决策边界修正（Weakly supervised decision boundary rectification，WDBR）
2. 弱监督条件下的特征漂移正则化（Weakly supervised feature drift regularization，WFDR）

Weakly supervised decision boundary rectification

WDBR基于一种朴素的思考：一般的数据集设定中，某一特定ID的人物，在不同的State下出现的图像应该是近乎均等的，如果某一代理类出现了过多某一状态下的图像样本，很可能是因为环境因素使得这一局部的决策边界未能得到合理划分。
基于这样的思考，WDBR引入了一种量化指标最大优势指数（Maximum Predominance Index，MPI），对于第 $k$ 个代理类，这一指数被定义如下
$R_k=\frac{\mathop{\max}_{j}|\mathcal{M}\cap\mathcal{Q}_j|}{|\mathcal{M}_k|}\in[0,1]\\ \mathcal{M}_k=\{x_i|\hat{y}_i=k\}\\ \mathcal{Q}_j=\{x_i|s_i=j\}$
WDBR进一步定义了一个修正因子 $p(k)=\frac{1}{1+\exp(a\cdot(R_k-b))}\in[0,1]$ ，其中 $a$ 为修正强度系数， $b$ 为修正阈值。引入了修正因子之后，代理类的判定被调整为
$\hat{y}=\mathop{\arg\mathop{\max}_{k}}p(k)\exp(x^\top \mu_{k})$
经过决策边界修正，修正因子也参与到了代理类的划分之中，定性分析，如果某一代理类下存在某一种状态的聚集，其MPI值会较大， $p(k)$ 值较小，这样在下一次迭代中这一代理类被选择的可能就会减小，位于决策边界的样本会更倾向于相邻的类别，经过这样的调整，两个代理类 $\mu_1$ 和 $\mu_2$ 的新决策边界会调整为
$(\mu_1-\mu_2)^\top x+\log\frac{p(1)}{p(2)}=0$

Weakly supervised feature drift regularization

WFDR考虑解决那些因为环境因素所带来的普遍影响，也引入了相似的思考，一般的数据集设定中，各种不同的State下出现的图像，其ID分布应该是近似相同的。
为了消去不同环境条件对编码带来的影响，WFDR希望让不同环境条件下的图像导出的编码能拥有近似的代理类分布。定义第 $j$ 类状态下的代理类分布是 $\mathbb{P}(\mathcal{Q}_j)$ ，定义全局代理类分布是 $\mathbb{P}(\mathcal{X})$ ，其中 $\mathcal{X}=f(\mathcal{U})$ 。此时，WFDR的目标是
$\mathop{\min}_{\theta}L_{drift}=\sum_{j}d(\mathbb{P}(\mathcal{Q}_j),\mathbb{P}(\mathcal{X}))$
式中 $d(\cdot,\cdot)$ 描述了两个分布之间的距离，其具体形式是一个二维Wasserstein距离，以 $m$ 和 $\sigma$ 描述分布的均值和标准差，上式中的距离可被展开为
$d(\mathbb{P}(\mathcal{Q}_j),\mathbb{P}(\mathcal{X}))=\|m_j-m\|_2^2+\|\sigma_j-\sigma\|_2^2$
WFDR的优化项是网络的参数，经过WFDR优化后，不同State下的图像样本会被编码为相似的分布，这样，因为环境因素带来的特征漂移，就会被最大程度的修正。